Inferências envolvendo duas populações normais

Source: vignettes/twosample.Rmd

Comparações de médias quando as variâncias populacionais conhecidas

Exemplo 10.1 (adaptado): Um engenheiro está interessado em desenvolver uma nova formulação para uma tinta. Duas formulações de tintas são testadas: a formulação 1, que tem uma química padrão, e a formulação 2, que possui um novo ingrediente para secagem (espera-se que essa nova formulação leve a redução do tempo médio de secagem). Com base em experimentos passados, o engenheiro sabe que o desivo-padrão do tempo de secagem é igual a 8 minutos, e que essa variabilidade não deve ser afetada pela adição do novo ingrediente. Dez espécimes são pintados com a formulação 1 e outros dez com a formulação 2, sendo a determinação da formulação utilizada para cada espécime feita de forma aleatória. Os dados desse experimento foram gerados artificialmente no R para fins de ilustração da parte computacional.

library(planex)
library(tidyverse)

# formato longo:
glimpse(tintas)
#> Rows: 20
#> Columns: 2
#> $ formulacao <chr> "F1", "F2", "F1", "F2", "F1", "F2", "F1", "F2", "F1", "F2",…
#> $ tempo      <dbl> 130.76740, 99.18879, 127.96217, 105.37315, 124.36982, 108.1…
data(tintas)
z.test(tempo~formulacao, sigma = 8, alternative = "greater", data = tintas)
#> 
#>  Two-sample z-test
#> 
#> data:  tintas
#> z = 2.7204, p-value = 0.00326
#> alternative hypothesis: true difference in means is greater than 0
#> 95 percent confidence interval:
#>  3.848103      Inf
#> sample estimates:
#> mean in group F1 mean in group F2 
#>         122.2223         112.4894


# formato largo:
data(tintas2)
glimpse(tintas2)
#> Rows: 10
#> Columns: 2
#> $ F1 <dbl> 130.7674, 127.9622, 124.3698, 104.6982, 135.3703, 130.9753, 109.996…
#> $ F2 <dbl> 99.18879, 105.37315, 108.18680, 121.52813, 104.04994, 114.23531, 12…

with(tintas2,
  z.test(x=F1, y=F2, sigma = 8, alternative = "greater")     
)
#> 
#>  Two-sample z-test
#> 
#> data:  F1 and F1
#> z = 2.7204, p-value = 0.00326
#> alternative hypothesis: true difference in means is greater than 0
#> 95 percent confidence interval:
#>  3.848103      Inf
#> sample estimates:
#> mean in group F1 mean in group F2 
#>         122.2223         112.4894

Alternativamente:

# mudando o nível de referência:
tintas <- tintas %>%
  mutate(
    formulacao = factor(formulacao, levels = c("F2", "F1"))
  )
levels(tintas$formulacao)
#> [1] "F2" "F1"
z.test(tempo~formulacao, sigma = 8, alternative = "less", data = tintas)
#> 
#>  Two-sample z-test
#> 
#> data:  tintas
#> z = -2.7204, p-value = 0.00326
#> alternative hypothesis: true difference in means is less than 0
#> 95 percent confidence interval:
#>       -Inf -3.848103
#> sample estimates:
#> mean in group F2 mean in group F1 
#>         112.4894         122.2223

with(tintas2,
  z.test(x=F2, y=F1, sigma = 8, alternative = "less")     
)
#> 
#>  Two-sample z-test
#> 
#> data:  F2 and F2
#> z = -2.7204, p-value = 0.00326
#> alternative hypothesis: true difference in means is less than 0
#> 95 percent confidence interval:
#>       -Inf -3.848103
#> sample estimates:
#> mean in group F2 mean in group F1 
#>         112.4894         122.2223

Exemplo 10.4 (adaptado): Testes de resistência à tensão foram feitos em dois tipos diferentes de estruturas de alumínio. Essas estruturas foram usadas na fabricação das asas de um avião comercial. De experiências passadas com o processo de fabricação dessas estruturas e com o procedimento de testes, os desvios-padrão são considerados conhecidos (σ1=1\sigma_{1} = 1 e σ2=1.5\sigma_{2} = 1.5, respectivamente). Os dados desse experimentos estão disponíveis no conjunto de dados aluminio do pacote planex. Obtenha um intervalo de confiança de 90% para a diferença das médias.


library(planex)
data(aluminio)

z.test(resistencia ~ estrutura, sigma = c(1, 1.5), conf.level = 0.9, data = aluminio)
#> 
#>  Two-sample z-test
#> 
#> data:  aluminio
#> z = 24.033, p-value < 2.2e-16
#> alternative hypothesis: true difference in means is not equal to 0
#> 90 percent confidence interval:
#>  12.00449 13.76840
#> sample estimates:
#> mean in group E1 mean in group E2 
#>         87.77779         74.89135


# fazendo as contas passo a passo:

sigma <- c(1, 1.5)
n <- c(10, 12)
alpha <- 0.1

medias <- with(aluminio, tapply(resistencia, estrutura, mean))
medias
#>       E1       E2 
#> 87.77779 74.89135
dbar <- medias[1]-medias[2]
V <- (sigma[1]^2)/n[1] + (sigma[2]^2)/n[2]
V
#> [1] 0.2875

ztab <- qnorm(alpha/2, lower.tail = FALSE)
epsilon <- ztab*sqrt(V)
li <- dbar - epsilon
ls <- dbar + epsilon
ic <- c(li, ls)
ic
#>       E1       E1 
#> 12.00449 13.76840

Comparações de variâncias

Sejam X11,...,X1n1X_{11}, ..., X_{1n_{1}} a.a. de X1∼N(μ1;σ12)X_{1}\sim N(\mu_{1};\sigma_{1}^{2}) e X21,...,X2n2X_{21}, ..., X_{2n_{2}} a.a. de X2∼N(μ1;σ12)X_{2}\sim N(\mu_{1};\sigma_{1}^{2}), com X1X_{1} e X2X_{2} independentes, com μ1,μ2,σ12\mu_{1},\mu_{2}, \sigma_{1}^{2} e σ22\sigma_{2}^{2} desconhecidos.

Considere as hipóteses:

{H0:σ12/σ22=1H1:σ12/σ22≠1\begin{eqnarray} { \left\{\begin{array}{lcc} H_{0}: \sigma_{1}^{2}/\sigma_{2}^{2}=1 \\ H_{1}: \sigma_{1}^{2}/\sigma_{2}^{2} \neq 1 \end{array}\right. } \nonumber \end{eqnarray}

Então, sob H0H_{0} segue que σ12=σ22=σ2\sigma_{1}^{2}=\sigma_{2}^{2}=\sigma^{2}. Logo,

(n1−1)S12σ2∼χn1−1 e (n2−1)S22σ2∼χn2−1\begin{eqnarray} \frac{(n_{1}-1)S_{1}^{2}}{\sigma^{2}} \sim \chi_{n_{1}-1} ~~~ \mbox{ e } ~~~ \frac{(n_{2}-1)S_{2}^{2}}{\sigma^{2}} \sim \chi_{n_{2}-1} \nonumber \end{eqnarray}

Consequentemente,

F0=S12S22∼F(n1−1;n2−1)\begin{eqnarray} F_{0}=\frac{S_{1}^{2}}{S_{2}^{2}} \sim F_{(n_{1}-1;n_{2}-1)} \nonumber \end{eqnarray}

Assim, RC={f0:f0<f(α2;n1−1;n2−1) ou f0>f(1−α2;n1−1;n2−1)}RC=\{f_{0}:f_{0}<f_{(\frac{\alpha}{2};n_{1}-1;n_{2}-1)} \mbox{ ou } f_{0}>f_{(1-\frac{\alpha}{2};n_{1}-1;n_{2}-1)}\}, em que

f0=s12s22\begin{eqnarray} f_{0}=\frac{s_{1}^{2}}{s_{2}^{2}} \nonumber \end{eqnarray}

é o valor observado da estatística do teste.

Cálculo do p-valor:

α*=2×min{p1,p2},\begin{eqnarray} \alpha^{*} = 2 \times \min\{p_{1}, p_{2}\}, \nonumber \end{eqnarray}

em que p1=P(F0<f0)p_{1}= P(F_{0}< f_0), p2=P(F0>f0)p_{2}= P(F_{0} > f_0).

Regiões críticas/cálculo de p-valores associadas testes de hipóteses com alternativas unilaterias são obtidas adaptando-se a região crítica apresentada acima.

Sabemos que F=σ12S22σ22S12∼F(n2−1;n1−1).\begin{eqnarray} F=\frac{\sigma_{1}^{2}S_{2}^{2}}{\sigma_{2}^{2}S_{1}^{2}} \sim F_{(n_{2}-1;n_{1}-1)}. \nonumber \end{eqnarray}

Logo, intervalos de confiança de 100(1−α)%100(1-\alpha)\% para σ12/σ22\sigma_{1}^{2}/\sigma_{2}^{2} são obtidos da seguinte forma:

1−α=P(fα2;n2−1,n1−1<σ12S22σ22S12<f1−α2;n2−1,n1−1)=P(S12S22fα2;n2−1,n1−1<σ12σ22<S12S22f1−α2;n2−1,n1−1),\begin{eqnarray} 1-\alpha &=& P\left(f_{\frac{\alpha}{2}; n_{2}-1, n_{1}-1} < \frac{\sigma_{1}^{2}S_{2}^{2}}{\sigma_{2}^{2}S_{1}^{2}} < f_{1-\frac{\alpha}{2}; n_{2}-1, n_{1}-1} \right) \nonumber \\ &=& P\left(\frac{S_{1}^{2}}{S_{2}^{2}}f_{\frac{\alpha}{2}; n_{2}-1, n_{1}-1} < \frac{\sigma_{1}^{2}}{\sigma_{2}^{2}} < \frac{S_{1}^{2}}{S_{2}^{2}}f_{1-\frac{\alpha}{2}; n_{2}-1, n_{1}-1} \right), \nonumber \end{eqnarray}

Intervalos de confiança unilaterais são obtidos de maneira direta a partir do desenvolvimento apresentado acima.

Exemplo 10.5: Dois catalisadores estão sendo analisados para determinar como eles afetam o rendimento médio de um processo quı́mico. Especificamente, o catalisador 1 (mais caro) está correntemente em uso, mas o catalisador 2 (mais barato) é aceitável. Uma vez que o catalisador 2 é mais barato, ele deve ser adotado, desde que não altere o rendimento do processo.
library(planex)
library(planex)

data(catalisadores2)
catalisadores2
#>      C1    C2
#> 1 91.50 89.19
#> 2 94.18 90.95
#> 3 92.18 90.46
#> 4 95.39 93.21
#> 5 91.79 97.19
#> 6 89.07 97.04
#> 7 94.72 91.07
#> 8 89.21 92.75

# testando a igualdade das variâncias:
with(catalisadores2, var.test(C1, C2))
#> 
#>  F test to compare two variances
#> 
#> data:  C1 and C2
#> F = 0.63907, num df = 7, denom df = 7, p-value = 0.5691
#> alternative hypothesis: true ratio of variances is not equal to 1
#> 95 percent confidence interval:
#>  0.1279433 3.1920724
#> sample estimates:
#> ratio of variances 
#>          0.6390651

Trabalhando com os dados em formato de pilha:

cat <- catalisadores2 %>%
  pivot_longer(
    cols = everything(),
    names_to = "catalisador",
    values_to = "rendimento"
  )

ggplot(cat, aes(x=catalisador, y = rendimento)) +
  geom_boxplot()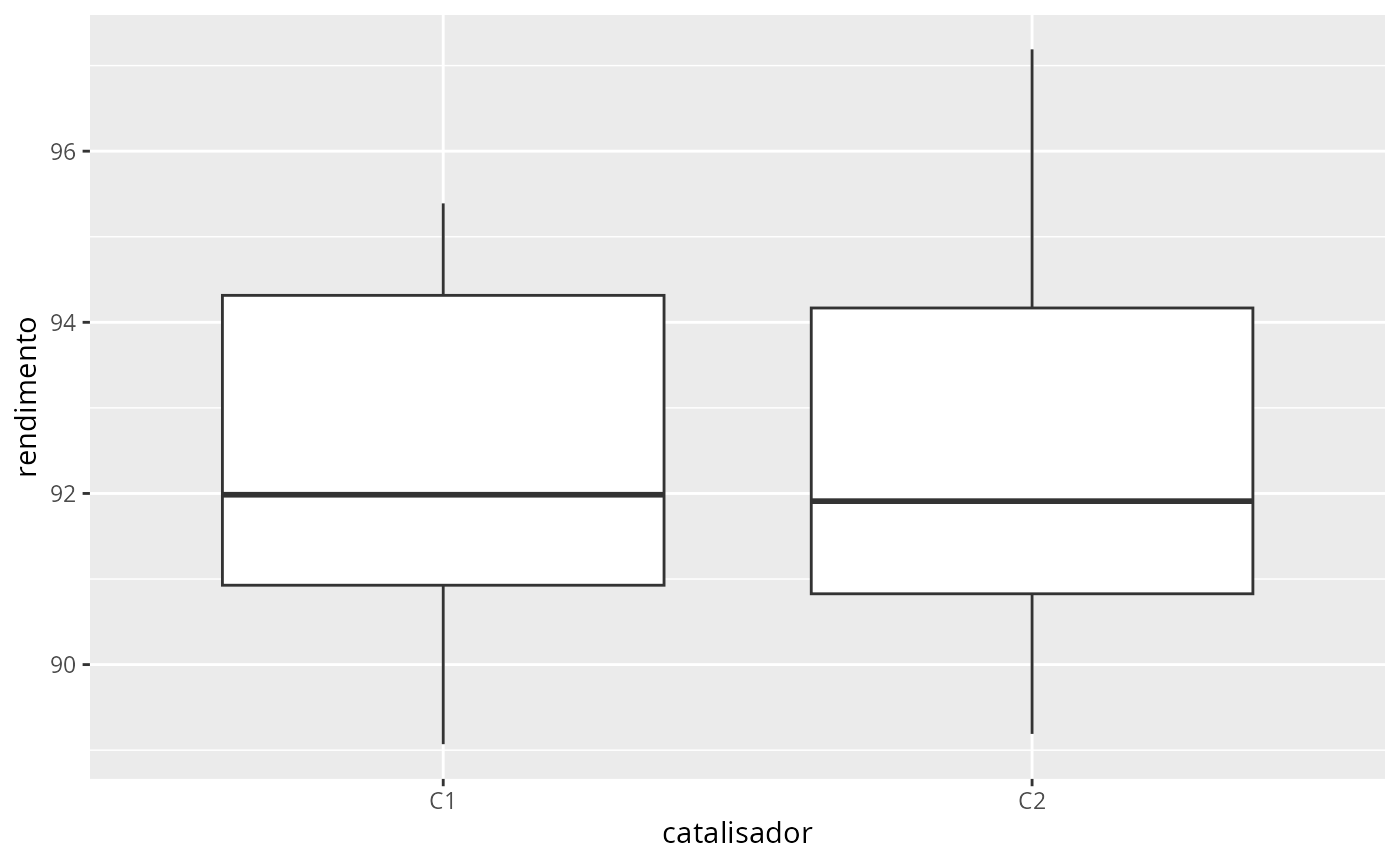


var.test(rendimento~catalisador, data = cat)
#> 
#>  F test to compare two variances
#> 
#> data:  rendimento by catalisador
#> F = 0.63907, num df = 7, denom df = 7, p-value = 0.5691
#> alternative hypothesis: true ratio of variances is not equal to 1
#> 95 percent confidence interval:
#>  0.1279433 3.1920724
#> sample estimates:
#> ratio of variances 
#>          0.6390651

Comparações de médias quando as variâncias populacionais iguais e desconhecidas 

t.test(rendimento~catalisador, data = cat, var.equal = TRUE)
#> 
#>  Two Sample t-test
#> 
#> data:  rendimento by catalisador
#> t = -0.35359, df = 14, p-value = 0.7289
#> alternative hypothesis: true difference in means between group C1 and group C2 is not equal to 0
#> 95 percent confidence interval:
#>  -3.373886  2.418886
#> sample estimates:
#> mean in group C1 mean in group C2 
#>          92.2550          92.7325

data(arsenio)
arsenio
#>    metrop rural
#> 1       3    48
#> 2       7    44
#> 3      25    40
#> 4      10    38
#> 5      15    33
#> 6       6    21
#> 7      12    20
#> 8      25    12
#> 9      15     1
#> 10      7    18

arsenio <- arsenio %>%
  pivot_longer(
    cols = everything(),
    names_to = "comunidade",
    values_to = "concentracao"
  )
arsenio
#> # A tibble: 20 × 2
#>    comunidade concentracao
#>    <chr>             <int>
#>  1 metrop                3
#>  2 rural                48
#>  3 metrop                7
#>  4 rural                44
#>  5 metrop               25
#>  6 rural                40
#>  7 metrop               10
#>  8 rural                38
#>  9 metrop               15
#> 10 rural                33
#> 11 metrop                6
#> 12 rural                21
#> 13 metrop               12
#> 14 rural                20
#> 15 metrop               25
#> 16 rural                12
#> 17 metrop               15
#> 18 rural                 1
#> 19 metrop                7
#> 20 rural                18

ggplot(arsenio, aes(x=comunidade, y=concentracao)) +
  geom_boxplot()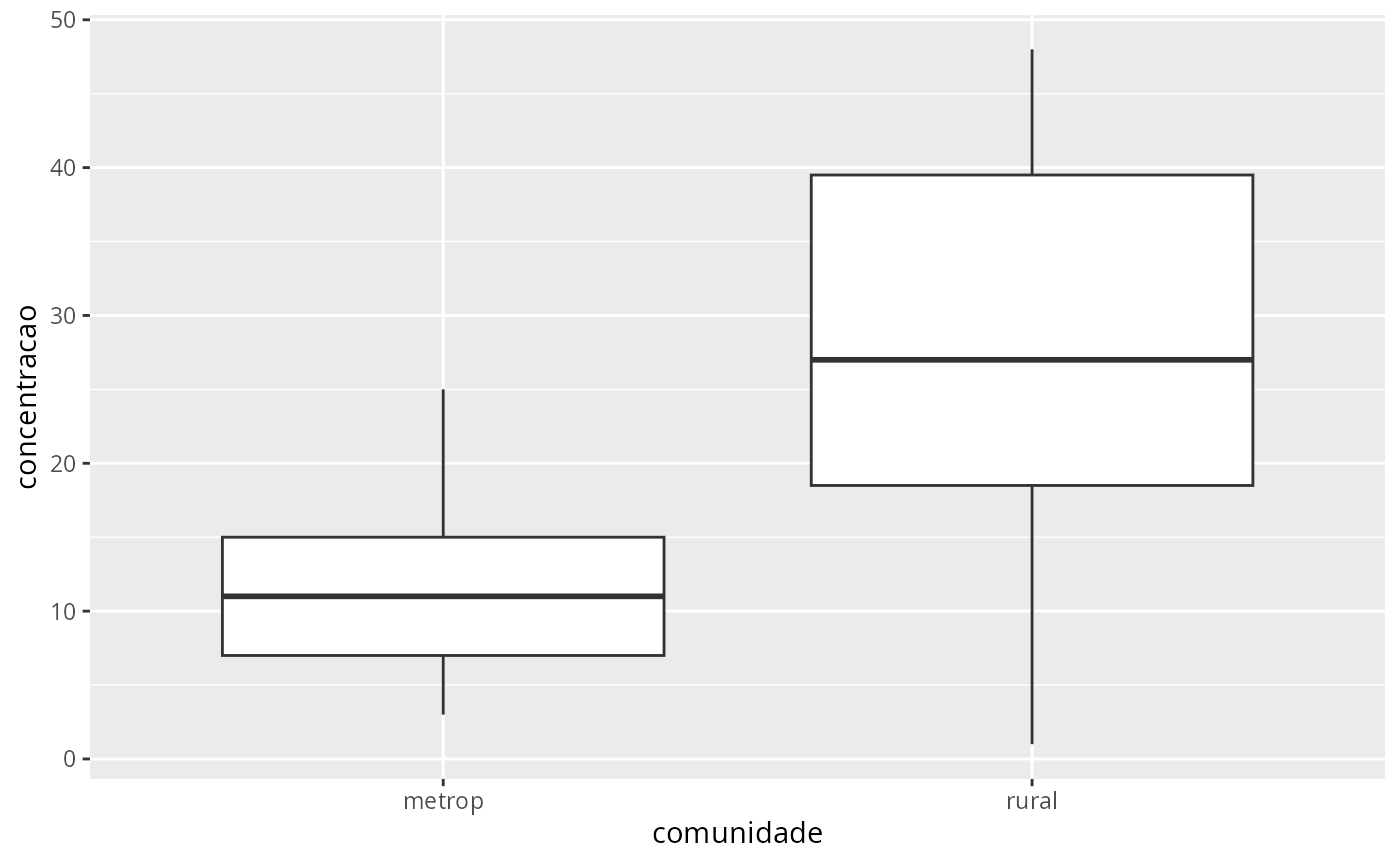


var.test(concentracao~comunidade, data=arsenio)
#> 
#>  F test to compare two variances
#> 
#> data:  concentracao by comunidade
#> F = 0.24735, num df = 9, denom df = 9, p-value = 0.04936
#> alternative hypothesis: true ratio of variances is not equal to 1
#> 95 percent confidence interval:
#>  0.06143758 0.99581888
#> sample estimates:
#> ratio of variances 
#>          0.2473473

t.test(concentracao~comunidade, data=arsenio)
#> 
#>  Welch Two Sample t-test
#> 
#> data:  concentracao by comunidade
#> t = -2.7669, df = 13.196, p-value = 0.01583
#> alternative hypothesis: true difference in means between group metrop and group rural is not equal to 0
#> 95 percent confidence interval:
#>  -26.694067  -3.305933
#> sample estimates:
#> mean in group metrop  mean in group rural 
#>                 12.5                 27.5
t.test(concentracao~comunidade, data=arsenio, var.equal = TRUE)
#> 
#>  Two Sample t-test
#> 
#> data:  concentracao by comunidade
#> t = -2.7669, df = 18, p-value = 0.0127
#> alternative hypothesis: true difference in means between group metrop and group rural is not equal to 0
#> 95 percent confidence interval:
#>  -26.389418  -3.610582
#> sample estimates:
#> mean in group metrop  mean in group rural 
#>                 12.5                 27.5